数学工房

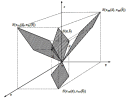
数学工房	Q&A 　お問い合わせ

数学工房よりお知らせ
【数学工房の会費及び講座料について】〔2023/8/22掲載〕　数学工房では、会費及び講座料につきまして消費税をいただいておりません。
【2025年会費について】 2025年会費（1月～12月） ¥3,000（学生 ¥1,500）を受け付けております。集中セミナー、通常講座、研究会のご参加に必要です〔会費未納の方は受講できません〕。講座にご参加の方は、講座料と一緒にお振込みになるのが便利です。会費は施設の維持や備品の費用の一部に使われます。ご協力をお願いします。　数学工房 ※お振込みの際には、「2025年会費」としてください。またお名前をお忘れなく。それ以前の未納分のある方は御一緒にお願いします。 ※数学工房の退会を希望される方は、連絡の上退会手続きをお願いします。
〔振込の場合の振込先〕銀行口座：三井住友銀行　清瀬支店　普通預金　口座番号　４５８５２５３　数学工房　桑野耕一郵便振替　００１５０－９－６８６５１５　数学工房

　今週の講座

今週開講の講座はありません

　会員限定の研究会について

左にある扉のアイコンをクリックすると、会員限定の研究会について詳細が見られます。

研究会の今後の日程について：
〔作用素環論研究会〕　５月３１日（土）１０：３０～１２：３０の予定です（仮決め、場所未定）。

　お知らせ

　中央大学の諏訪紀幸先生にお話しいただきました、お年玉講義「数学の楽しみ方～フィボナッチ数列を題材にして」（2019年1月13日開催）のレジュメを掲載いたします。こちらよりご覧ください。
また、追加資料がございますので、あわせて掲載いたします。こちらよりご覧ください。

　「数学セミナ－」（日本評論社発行）2013年7月号に、「おとなが勉強したいときに読む数学書」という題で、学部や修士程度の数学を学んだことのある人が、数学を勉強しなおすのに手頃な数学書の紹介をしておきました。

エレガントな解答を求む！！
数学セミナー(日本評論社）２００９年８月号の「エレガントな解答を求む」の出題の詳細な解説です。会員の方にも参考になると思います。是非、一度ご覧下さい。
問題	解答と解説

数学の稽古法を追求してきた著者の、１６年にわたるあゆみを伝えるドキュメント「数学講義のデザイン　数学工房の稽古の源流」の紹介。	今月のスケジュールです。
数学工房では、年３回会報を発行しています。２００６年７月会報No.84からのバックナンバーです。	名古屋公開講座の記録です。一部の講座については講義ノートを公開しています。